How to read pressure regulator flow rate chart?

Principle and application of pressure regulators

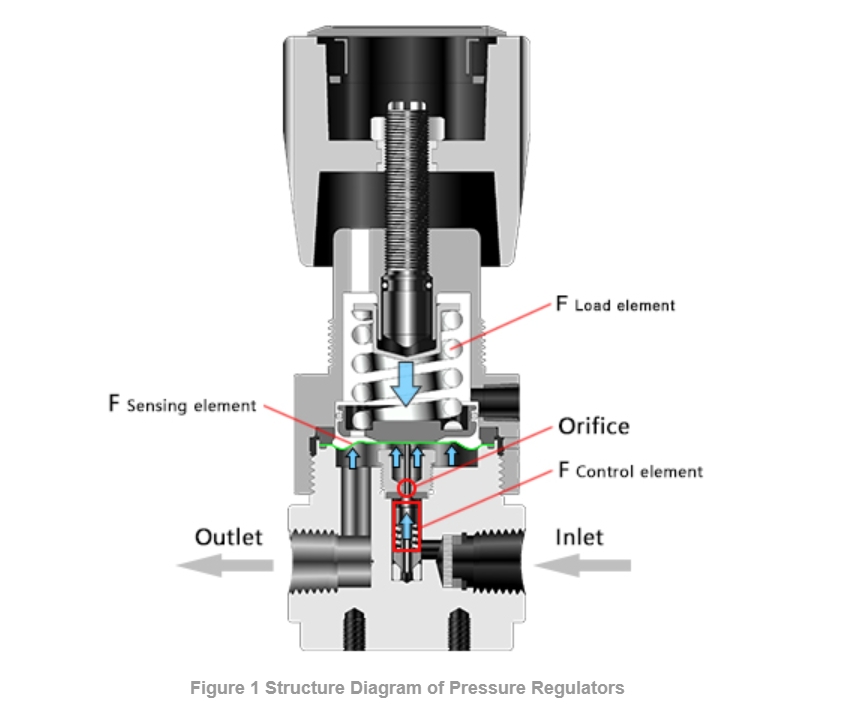
A pressure-reducing valve operates based on a unique flow passage structure (as shown in Figure 1). When high-pressure fluid enters and flows through the throttle orifice, the fluid's velocity increases and its pressure decreases, achieving the desired pressure reduction. Additionally, the valve can regulate the spring load to balance the fluid loads generated by the inlet and outlet pressures, thereby controlling the outlet pressure and maintaining it at a constant level. This force balance is described by Equation (1).

Fload element = Fsensing element + Fcontrol element Formula (1)

Where:

Fload element = range spring load

Fsensing element = outlet pressure × diaphragm effective area

Fcontrol element = inlet pressure × poppet effective area + poppet spring load

The primary function of pressure regulators is to lower the upstream inlet pressure to a predetermined outlet pressure and maintain that level, ensuring the system meets specific pressure requirements. Pressure regulators are extensively used in applications involving special gases and high-purity systems.

Composition and function of a flow chart

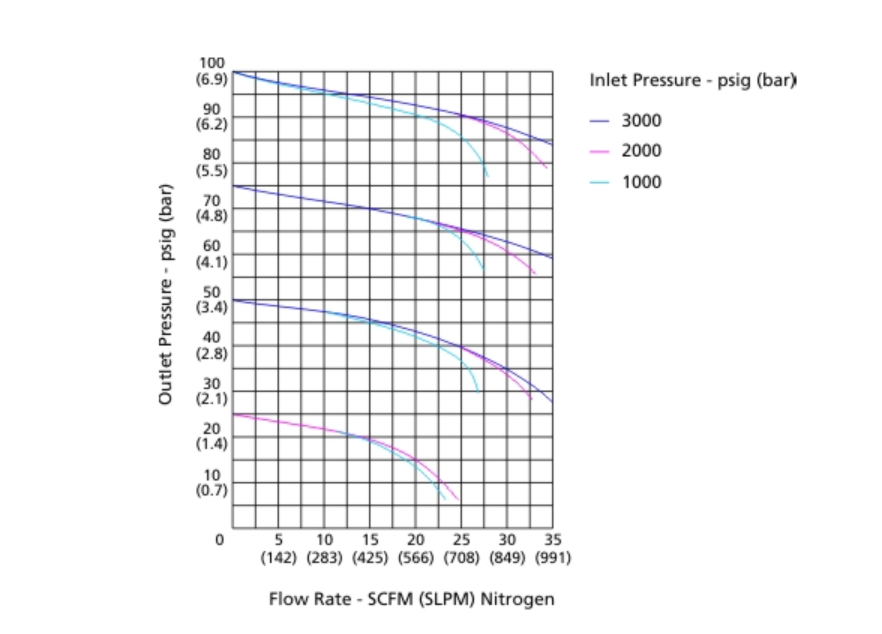
The flow curve (as shown in Figure 2) illustrates the relationship between flow rate (horizontal axis) and outlet pressure (vertical axis) at a given inlet pressure for a pressure regulator. This curve reveals how the pressure regulator responds to changes in system flow rate, depicting the range of system pressures that the regulator can maintain at specified flow rates.

How to Use a Flow Chart?

Valve manufacturers typically provide multiple flow curves for the same series of regulators at different inlet pressures but the same outlet pressure to illustrate the operating range of the regulator. As shown in Figure 2, the horizontal axis represents the flow rate, the vertical axis represents the outlet pressure, and different colored curves represent various inlet pressures, such as 3000 psig (206.8 bar), 2000 psig (137.9 bar), and 1000 psig (68.9 bar). When the flow rate is zero, the outlet pressure on the vertical axis corresponds to the set outlet pressure.

The flow curve demonstrates a "droop" trend, meaning that under a specific inlet pressure and set outlet pressure, the outlet pressure gradually decreases as the flow rate increases. Due to limitations in the internal structure and components, pressure regulators cannot maintain a perfectly horizontal flow curve in any given regulating state. Consequently, as the flow rate increases, the outlet pressure decreases to some extent.

For applications of pressure regulators, it is generally required to maintain a relatively constant outlet pressure despite significant changes in system flow. Therefore, the less droop observed in the flow curve, the better the performance of the pressure regulator.

How to Use a Flow Chart

For a specific type of pressure regulator, first locate the corresponding flow chart and select the curve that matches the actual inlet pressure and set outlet pressure values. Then, using the horizontal axis flow rate scale, find the corresponding point on the curve and determine the actual outlet pressure at that point from the vertical axis. If the required pressure condition is not represented in the provided flow chart, a new curve can be interpolated between two adjacent existing curves.

Additionally, the flow chart provided by the manufacturer is based on test conditions using nitrogen as the test medium at a temperature of 70℉ (20°C). If the actual system uses a different medium or operates at a different temperature, the flow rate scale on the horizontal axis of the flow chart should be adjusted according to formula (2), while the overall trend of the curve remains unchanged.

Q₂ = Q₁ X F_G X F_T Formula (2)

In the formula, Q1 is the initial flow rate scale, Q2 is the modified flow rate scale, FG is the gravity modified coefficient, FT is the temperature modified coefficient. The values of FG and FT can be referred to in Table 1 and Table 2 respectively.

Table 1

Medium Type	Gravity Modified Coefficient ( FG )
Arsine	0.60
Carbon dioxide	0.80
Argon	0.84
Hydrogen chloride	0.87
Silane	0.93
Oxygen	0.94
Air	0.98
Ammonia gas	1.28
Helium	2.65
Hydrogen	3.72

Table 2

Temperature(°F)	Temperature(℃)	Temperature Modified Coefficient(FT)
-40	-40	1.12
-20	-28	1.10
0	-17	1.07
20	-6	1.05
70	20	1.00
100	37	0.97
150	65	0.93
212	100	0.89
250	121	0.86
300	148	0.84
350	176	0.81
400	204	0.78

By reading the pressure regulator flow curve, you can intuitively determine whether the selected regulator meets the actual system conditions (pressure, flow rate, etc.), enabling quick selection.

Application Examples

Since the customer's medium type and operating temperature differ from the test medium and temperature used in the manufacturer's flow chart, the flow rate scale needs to be adjusted using the gravity modification coefficient (FG) and the temperature modification coefficient (FT). According to Table 1, when the medium is carbon dioxide, the gravity modification coefficient FG is 0.80. From Table 2, at a temperature of 100°F (37°C), the temperature modification coefficient FT is 0.97. By applying the initial flow rate scale (i.e., the horizontal axis value) from Figure 4 along with FG and FT into formula (2), the adjusted flow rate scale can be calculated (example: 3.9 = 5 x 0.8 x 0.97). Replace the horizontal axis in Figure 4 with this adjusted flow rate scale while keeping the vertical axis and flow curve unchanged to create a new flow chart, as shown in Figure 5.

As shown in Figure 5, the flow curve for the customer's desired inlet pressure of 3000 psig (206.8 bar) and outlet set pressure of 90 psig (6.2 bar) is not provided. To obtain this curve, we can interpolate between the two flow curves for an inlet pressure of 3000 psig (206.8 bar) with outlet set pressures of 75 psig (5.2 bar) and 100 psig (6.9 bar). This interpolation yields the flow curve for an inlet pressure of 3000 psig (206.8 bar) and an outlet set pressure of 90 psig (6.2 bar), as shown by the red curve in Figure 6.

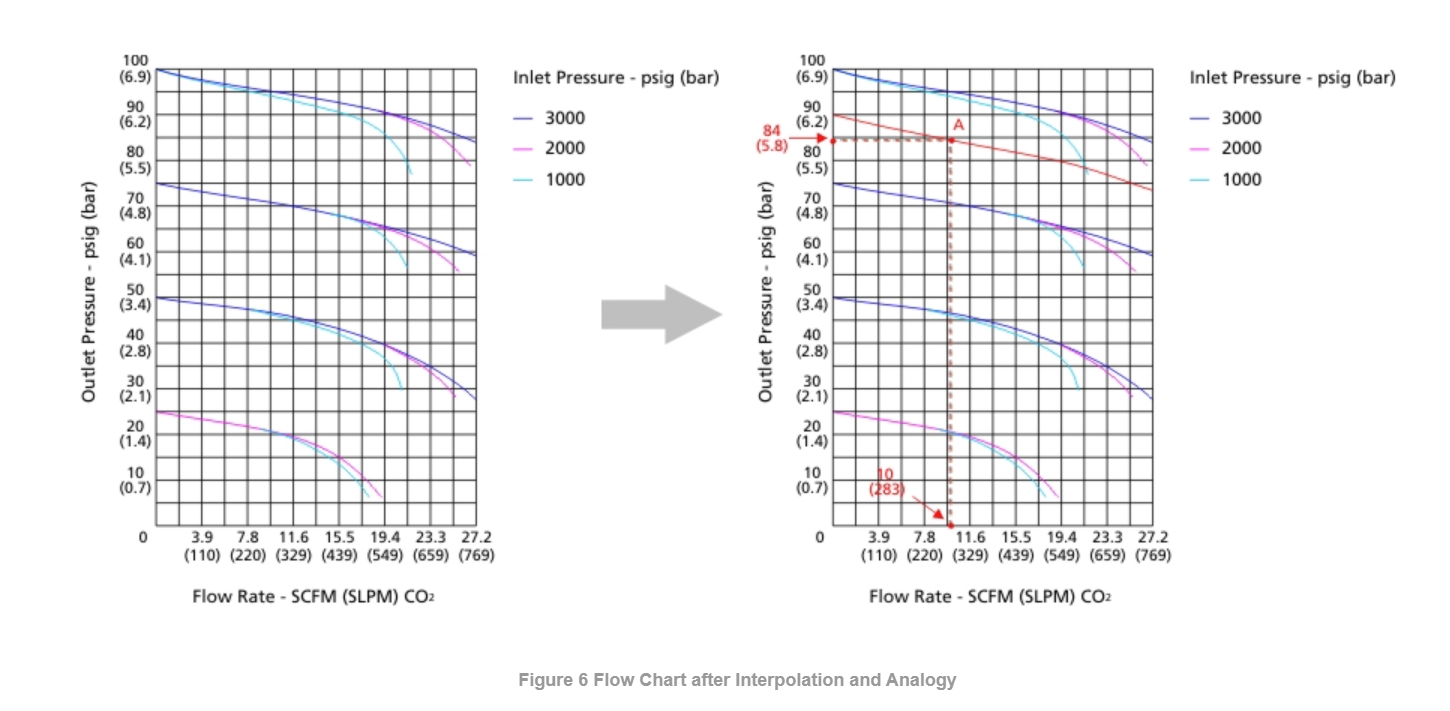
From the flow curve (red curve) shown in Figure 6 for an inlet pressure of 3000 psig (206.8 bar) and an outlet set pressure of 90 psig (6.2 bar), locate point A on the curve at a flow rate of 10 SCFM (283 SLPM) on the horizontal axis. From the vertical axis, determine the actual outlet pressure, which is 84 psig (5.8 bar).

Therefore, for FCR-1S series pressure regulators with an inlet pressure of 3000 psig (206.8 bar), an outlet set pressure of 90 psig (6.2 bar), an operating temperature of 100°F (37°C), and a system medium (CO2) flow rate of 10 SCFM (283 SLPM), the actual outlet pressure is 84 psig (5.8 bar).

Conclusion

By properly utilizing the pressure regulator flow chart, we can determine if the selected regulator meets the customer's working pressure requirements, enabling rapid and accurate part number selection. Additionally, the flow chart provides insight into the pressure regulating performance of the regulators.